略典。
原题链接
给定一个 个点的简单无向图,求图中如下子图的数量, 组数据:
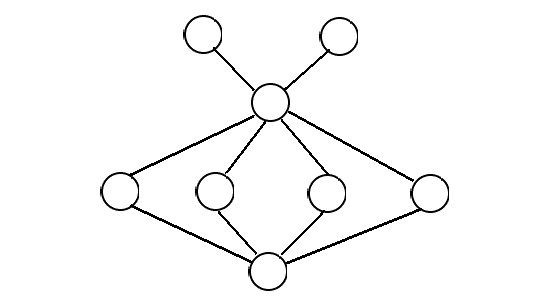
形式化地,给定简单无向图 ,求子图 的数量,其中 满足
注意到 和 的位置比较关键。
考虑枚举 和 ,求它们直接连接的点集的交,任取 个 构成 。
从剩下的 直接连接的点(若包含 ,将其排除)中任取 个,构成 。
然后就是组合数学的计算了。
使用 bitset 加速,复杂度 。
dynamic_bitset 的 Bug 对计算没有影响。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include <cstdint>
#include <iostream>
#include <tr2/dynamic_bitset>
#include <vector>
using namespace std;
using tr2::dynamic_bitset;
static constexpr uint32_t Mod = 1'000'000'007;
template <uint32_t Mod> struct Comb {
vector<uint32_t> fac, ifac;
Comb(uint32_t n) : fac(n + 1), ifac(n + 1) {
fac[0] = 1;
for (uint32_t i = 1; i <= n; ++i)
fac[i] = (uint64_t)fac[i - 1] * i % Mod;
ifac[n] = inv(fac[n]);
for (uint32_t i = n; i > 0; --i)
ifac[i - 1] = (uint64_t)ifac[i] * i % Mod;
}
uint64_t inv(uint32_t a) {
uint64_t base = a % Mod, res = 1, exp = Mod - 2;
for (; exp; exp >>= 1, (base *= base) %= Mod)
if (exp & 1)
(res *= base) %= Mod;
return res;
}
uint32_t operator()(uint32_t n, uint32_t k) {
if (k > n)
return 0;
return (uint64_t)fac[n] * ifac[k] % Mod * ifac[n - k] % Mod;
}
};
Comb<Mod> comb(1'003);
void solve() {
size_t n, m;
cin >> n >> m;
vector<size_t> deg(n);
vector<dynamic_bitset<>> a(n, dynamic_bitset<>(n));
for (size_t i = 0; i < m; ++i) {
size_t u, v;
cin >> u >> v;
--u, --v;
a[u][v] = a[v][u] = true;
++deg[u], ++deg[v];
}
uint32_t ans = 0;
for (size_t i = 0; i < n; ++i) {
for (size_t j = 0; j < n; ++j) {
if (i == j)
continue;
size_t x = (a[i] & a[j]).count();
size_t y = deg[i] - a[i].test(j);
if (x < 4 || y < 6)
continue;
(ans += (uint64_t)comb(x, 4) * comb(y - 4, 2) % Mod) %= Mod;
}
}
cout << ans << '\n';
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
size_t T;
cin >> T;
while (T--)
solve();
return 0;
}
|
